目前正在進行的橢圓曲線密碼學40年回顧： 🤓

呵呵，Neal Koblitz 談到「證明的外觀讓人印象深刻」以及「人們對數學的看法太膚淺」🤘

尼爾強調了美國反智主義的增加。

史蒂文·加爾布雷斯："基本上，ECC在40年的密碼分析中表現得比我們所希望的還要好。" 維克多·米勒："我很高興的是[...], 除了假設的量子電腦，它表現得很好。"

尼爾·科布利茨大致上表示，我們應該對假設尚未經過實際計算嘗試破解的問題的難度持懷疑態度。 （他早些時候提到LWE簡化存在巨大的差距。）

維克多·米勒："沒有太多人在研究同源性加密分析。" 史蒂文·加爾布萊斯（笑著從椅子上站起來）："我在，我在！"

Galbraith: "對學生的建議？" Victor Miller: "你必須對某件事情真正充滿熱情。所以選擇一個真正能引起你共鳴的東西！[...] 即使它看起來與任何事情都無關。[...] 這會有回報的"

尼爾·科布利茲（Neal Koblitz）：「在數學轉向密碼學的過程中，你需要一些批判性思維能力。危險在於分析的表面化。 養成這種[批判性思維]的習慣將防止你犯下嚴重錯誤或忽視他人。」

Dan Boneh 建議這本由 Bashmakova 所著的《Diophantus 和 Diophantine 方程式》書籍 👇

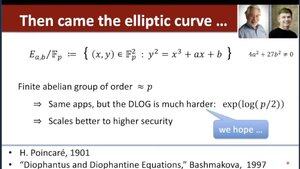
...而丹提到我對配對的歷史總結： 🫡🥲🥹

而且，自然地，簡單、美麗且極其多功能的 BLS 簽名方案 👇

（不知羞恥的推廣：你應該（幾乎）總是使用更快的 t\log^2{t} 時間算法來聚合 t-out-of-n BLS 簽名：）

Dan 提到 Boneh-Boyen 簽名，這種簽名不需要哈希，但需要更強的假設 👇

Dan 提醒我們，tau 的力量使得計算 tau 上的離散對數變得更容易 👇

Dan 要求我們所有人不要停下來，繼續研究多線性映射，這項技術現在至少已有 23 年的歷史！ 「我幾乎相信地球上有某個人知道答案，但我們還沒有找到那個人。」

Dan: "當我們談論後量子時，我們必須將其分為 _加密_ 和 _其他一切._" "對於加密，由於收割-現在-和-稍後解密攻擊，快速過渡是很重要的。" "對於完整性機制，仍然有相當多的時間。"

Dan 提醒大家，任何建造量子電腦的人都可以獲得巨大的蜜罐： 中本聰最初的（目前未花費的）比特幣！

"我非常支持混合的 [後量子] 部署。我們實際上已經看到一些 NIST [後量子] 候選者，甚至一些決賽選手在 **前**-量子攻擊下被破解。"

丹說「[我們需要] 鼓勵人們研究後量子安全的後量子[加密]系統」，並提醒我們最近的 LWE 恐慌，因為一個潛在的量子算法（幸運的是，最終被證明是錯誤的）。

Galbraith 將 80 年代的 8 頁 CRYPTO 論文與今天的 34 頁 CRYPTO 提交進行比較。 Dan: "某個時刻會有事情發生。我們的社群正在成長。越來越多的人進行研究 => 更多的論文 => 對委員會、論文作者和每個人都帶來更多壓力。我 會將這視為社群的成功。我會慶祝這一點。 如何應對這種增長？每個成功的領域都經歷過並應對過這種情況（例如，機器學習）。我相信我們會應對這一切。"

（脫離上下文）丹：「更努力工作。」

Kristin Lauter 談 Microsoft 的 ECC 歷史 👇

ECC 首次在 2005 年的 Windows Vista 中部署。 哦，那些早期互聯網的日子是多麼美好啊... 🥹🥹

Kristin Lauter: "BLS 簽名可以用來防止像 BitTorrent 這樣的 CDN 中的污染攻擊" 👇

Kristin Lauter 談量子威脅 👇 "當 m = 256 時，您需要大約 1,500 個 [邏輯、高保真度] 量子位於量子電腦上。"

Kristin Lauter 談到基於同源性的密碼學，這是由 Steven Galbraith 在 '05 年引入的 👇

....好吧，這就是回顧的結束（請參見完整計劃）！ 我向所有勇敢的智者致敬 🫡，是你們讓我們走到這一步，我迫不及待想要那些該死的多線性映射準備好，這樣我就可以建立我的 SMURFs 😆：

哦，但等等，我錯過了維克多·米勒的演講！😭 讓我看看我是否能總結一些那裡的精華...

Victor Miller 開場引用了一句好話："機會偏愛有準備的頭腦！" 👌👌 我的解釋：那麼，盡可能多地閱讀加密貨幣論文和數學教科書？

"有趣的是，當我到哈佛時，我當時是那裡唯一一位真正擅長計算的研究生。" 不要感到孤單。

這麼多數學家。 我從來不理解對於避免死亡的痴迷，但如果有任何理由……那就是不想在數學上失去進展！ （如果有更簡單的費馬最後定理的證明呢？）

Victor 提到 Coppersmith DL 演算法用於 GF(2^n)，以及他如何開始思考解決方法...

為什麼我們現在都能在 1 毫秒內驗證 zkSNARKs 👇

顯然，在2000年，有些人認為橢圓曲線密碼學是一個迷因。 我說，這對區塊鏈來說是個好消息！

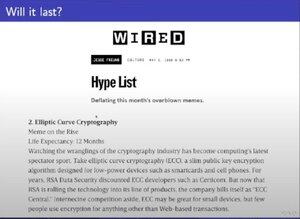
維克多總結道，研究像橢圓曲線或數論這樣的深奧事物總是好的。 你永遠不知道十年後什麼會實際上變得有用或實用。

回到 Neal Koblitz 的演講：他在 1979 年因為對 RSA 的教學好奇而首次接觸密碼學！ 他想更好地激勵他的數論課程，認為 RSA 是一個很好的方法！💕

後來，Lenstra 的橢圓曲線因式分解算法真正吸引了 Koblitz 👇

所以，Koblitz 開始思考：我能否使用這些花哨的代數幾何物件來*構建*（而不是破壞）密碼學？

Koblitz 回憶起早期從事加密貨幣的時候，這是一種反叛的行為。 這種活力和自由精神顯而易見： 例如，在 CRYPTO 講座的會議上，"限制" 意味著你只能向講者扔 *空的* 啤酒罐 😂😂

這當然已經改變了。 但是，正如丹·博內赫早些時候所說，這應該被視為一個成功，表明我們的領域已經起飛！

好吧，好吧，這真的結束了！ 🫡 在這裡查看兩個錄音： 完整的節目在這裡：