关于椭圆曲线密码学的40年回顾正在进行中： 🤓

嘿嘿，Neal Koblitz 讲述了 "证明的外观给人留下深刻印象" 和 "人们对数学的理解太肤浅了" 🤘

尼尔强调了美国反智主义的增加。

史蒂文·加尔布雷斯："基本上，ECC在40年的密码分析中表现得比我们所希望的要好。" 维克托·米勒："我很高兴的是[...], 除了一个假设的量子计算机，它表现得很好。"

尼尔·科布利茨大致表示，我们应该对假设尚未经过实际计算尝试破解的问题的难度持怀疑态度。 （他早些时候指出，LWE 归约存在巨大的差距。）

维克多·米勒："没有太多人在研究同态加密的密码分析。" 史蒂文·加尔布雷斯（笑着从椅子上站起来）："我在，我在！"

Galbraith: "对学生的建议？" Victor Miller: "你必须对某件事真正充满热情。所以选择一些真正与你产生共鸣的东西！[...] 即使它看起来与任何事情都没有关系。[...] 这会有回报的"

尼尔·科布利茨："在从数学到密码学的过程中，你需要一些批判性思维能力。危险在于分析的肤浅。 养成这种[批判性思维]的习惯将防止你犯严重错误或忽视他人。"

Dan Boneh 推荐这本由 Bashmakova 编写的《丢番图与丢番图方程》书籍 👇

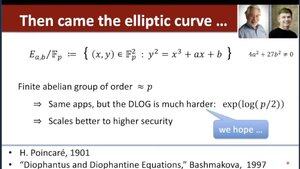
...而丹提到了我关于配对的历史总结： 🫡🥲🥹

而且，自然，简单、美丽且极其多功能的BLS签名方案👇

（无耻的宣传：你几乎总是应该使用更快的 t\log^2{t} 时间算法来聚合 t-out-of-n BLS 签名：）

Dan提到Boneh-Boyen签名，这种签名不需要哈希，尽管它们需要更强的假设👇

Dan 提醒我们，tau 的幂使得计算 tau 上的离散对数变得更容易 👇

丹要求我们所有人不要停下来，继续研究多线性映射，这项技术现在至少已有23年历史！ “我几乎相信地球上有人知道答案，但我们还没有找到那个人。”

丹："当我们谈论后量子时，我们必须将其分为_加密_和_其他一切._" "对于加密，由于收割后解密攻击，快速过渡是很重要的。" "对于完整性机制，仍然有相当多的时间。"

Dan提醒大家，任何构建量子计算机的人都可以获得巨大的蜜罐： 中本聪的初始（目前未花费的）比特币！

"我非常支持混合[后量子]部署。实际上，我们已经看到一些NIST [后量子]候选者，甚至一些决赛选手在**量子前**攻击中被攻破。"

丹说“[我们需要] 鼓励人们研究后量子[加密]系统的后量子安全性”，并提醒我们最近的LWE恐慌以及一个潜在的量子算法（幸运的是，结果是错误的）。

加尔布雷斯将80年代的8页CRYPTO论文与今天的34页CRYPTO提交进行了比较。 丹："总有一天会出现问题。我们的社区正在增长。更多的人进行研究 => 更多的论文 => 对委员会、论文作者和每个人的压力都在增加。我 会将此视为社区的成功。我会为此庆祝。 如何应对这种增长？每个成功的领域都经历过并应对过这种情况（例如，机器学习）。我相信我们会处理好这个问题。"

（脱离上下文）丹："更努力工作。"

Kristin Lauter谈微软ECC的历史👇

ECC首次在2005年的Windows Vista中部署。 哦，早期互联网的那些日子是多么美好啊... 🥹🥹

Kristin Lauter: "BLS 签名可以用来防止像 BitTorrent 这样的 CDN 中的污染攻击" 👇

Kristin Lauter谈量子威胁 👇 "当m = 256时，您需要大约1,500个[逻辑、高保真]量子比特在量子计算机上。"

Kristin Lauter 讨论了由 Steven Galbraith 在 2005 年引入的同源性基础密码学 👇

....aaaand 这就是回顾的总结（请参见完整程序）！ 我向所有勇敢的智者致敬 🫡，感谢他们让我们走到今天，我迫不及待想要那些该死的多线性映射准备好，这样我就可以构建我的 SMURFs 😆：

哦，但等等，我错过了维克托·米勒的演讲！😭 让我看看我能否总结一些精彩的内容...

维克多·米勒以一句美好的名言开场："机会青睐有准备的头脑！" 👌👌 我的理解是：那么，尽可能多地阅读加密货币论文和数学教科书？

"有趣的是，当我到达哈佛时，我当时是那里唯一一个真正具备计算能力的研究生。" 不要感到孤单。

这么多数学家。 我从来不理解对避免死亡的痴迷，但如果真有理由……那就是为了不在数学上失去进展！ （如果有一个更简单的费马大定理的证明呢？）

Victor提到了Coppersmith DL算法用于GF(2^n)，以及他是如何开始考虑解决方法的...

为什么我们现在都能在1毫秒内验证zkSNARKs 👇

显然，在2000年，一些人认为椭圆曲线密码学是一个玩笑。 我认为这对区块链来说是个好消息！

维克托总结道，研究一些深奥的事物，比如椭圆曲线或数论，总是好的。 你永远不知道十年后什么会变得实际或有用。

回到尼尔·科布利茨的演讲：他在1979年因对RSA的教学好奇而首次接触密码学！ 他想更好地激励他的数论课程，认为RSA是一个很好的方法！💕

后来，Lenstra 的椭圆曲线因式分解算法真正吸引了 Koblitz 👇

所以，Koblitz 开始思考：我能否使用这些花哨的代数几何对象来*构建*（而不是破坏）密码学？

Koblitz 回忆起早期做加密货币是一种反叛的行为。 这种活力和自由精神展现得淋漓尽致： 例如，在 CRYPTO 会议的休息环节中，"限制"意味着你只能向演讲者扔 *空* 啤酒罐 😂😂

当然，这已经改变了。 但是，正如丹·博内赫早些时候所说，这应该被视为一个成功，表明我们的领域已经起飞！

好吧，好吧，这真的是结束了！ 🫡 在这里查看两个录音： 完整程序在这里：