40letá retrospektiva kryptografie eliptických křivek právě probíhá: 🤓

Hehehe, Neal Koblitz hovoří o tom, jak "vzhled důkazu na lidi zapůsobí" a jak "přístup lidí k matematice je příliš povrchní" 🤘

Neal zdůrazňuje nárůst antiintelektualismu v USA.

Steven Galbraith: "ECC v podstatě obstálo tolik, v kolik jsme mohli doufat za 40 let kryptoanalýzy." Victor Miller: "Jsem potěšen, že [...], až na hypotetický kvantový počítač, to vydrželo."

Neal Koblitz zhruba říká, že bychom měli být skeptičtí k předpokladu tvrdosti problémů, které nezaznamenaly praktické výpočetní pokusy o její prolomení. (Dříve poukázal na to, že redukce LWE mají obrovské mezery.)

Victor Miller: "Není příliš mnoho lidí, kteří by pracovali na kryptoanalýze isogenií" Steven Galbraith (se smíchem vstává ze židle): "Jsem, já jsem!"

Galbraith: "Rada pro studenty?" Victor Miller: "Musíte být pro něco opravdu nadšení. Jděte tedy s něčím, co vás opravdu osloví! [...] I když to nevypadá, že by to mělo s něčím společného. [...] Vyplatí se to."

Neal Koblitz: "Při přechodu od matematiky ke kryptografii potřebujete určitou schopnost kritického myšlení. Nebezpečí spočívá v povrchnosti analýzy. Zvyk dělat to [kritické myšlení] vám zabrání dělat vážné chyby nebo přehlížet ostatní."

Dan Boneh doporučuje tuto knihu "Diofantovy a diofantické rovnice" od Bashmakové 👇

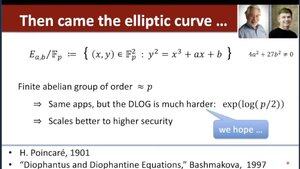
... a Dan zmiňuje můj historický přehled o párování: 🫡🥲🥹

A samozřejmě jednoduché, krásné a extrémně všestranné schéma podpisu 👇 BLS

(Nestydatá zástrčka: Měli byste (téměř-)vždy agregovat t-out-of-n BLS podpisy pomocí rychlejšího algoritmu t\log^2{t}-time: )

Dan zmiňuje Boneh-Boyenovy podpisy, které nevyžadují hašování, i když potřebují silnější předpoklad 👇

Dan nám připomíná, že powers-of-tau usnadňují výpočet diskrétního logu na tau 👇

Dan nás všechny žádá, abychom se nezastavovali a nepracovali na multilineárních mapách, které jsou nyní nejméně 23 let staré! "Jsem téměř přesvědčen, že někdo na planetě zná odpověď, a my jsme takovou osobu ještě nenašli."

Dan: "Když mluvíme o postkvantovém, musíme to rozdělit na _šifrování_ a _everything else._" "Pro šifrování, kvůli útokům typu "sklízej teď a dešifruj později", je důležité, abychom přešli rychle." "Na mechanismy integrity je stále dost času."

Dan všem připomíná obrovský hrnec medu, který je k dispozici každému, kdo staví kvantový počítač: Satoshiho počáteční (v současné době neutracené) bitcoiny!

"Jsem velmi silným zastáncem hybridního [postkvantového] nasazení. Ve skutečnosti jsme viděli řadu kandidátů NIST (post-kvantového), dokonce i některé z finalistů, kteří byli zlomeni **pre**-kvantovým útokem."

Dan říká: "[Potřebujeme] povzbudit lidi, aby studovali postkvantovou bezpečnost postkvantových [kryptografických] systémů" a připomíná nám nedávné zděšení LWE s potenciálním kvantovým algoritmem (který se naštěstí nakonec ukázal jako chybný).

Galbraith porovnává 8stránkové dokumenty CRYPTO z 80. let s dnešními 34stránkovými dokumenty CRYPTO. Dan: "Něco se v určitém okamžiku zlomí. Naše komunita se rozrůstá. Více lidí provádějících výzkum = > více článků = > větší tlak na výbory, na autory článků, na všechny. Já by to považoval za úspěch komunity. To bych oslavila. Jak se s tímto růstem vypořádat? Každý úspěšný obor ho měl a řešil ho (např. strojové učení). Věříme, že se s tím vypořádáme."

(Mimo kontext) Dan: "Pracuj tvrději."

Kristin Lauter o historii ECC ve společnosti Microsoft 👇

ECC bylo poprvé nasazeno ve Windows Vista v roce 2005. Ach, jak skvělé byly ty dny raného internetu... 🥹🥹

Kristin Lauter: "Podpisy BLS lze použít k prevenci útoků znečištění v CDN, jako je BitTorrent" 👇

Kristin Lauter o kvantové hrozbě 👇 "S m = 256 se díváte na to, že na kvantovém počítači potřebujete zhruba 1 500 [logických, vysoce věrných] qubitů."

Kristin Lauter o kryptografii založené na isogeny, kterou představil Steven Galbraith v roce 2005 👇

.... aaaa tím retrospektiva končí (celý program najdete zde)! Zdravím 🫡 všechny statečné intelekty, kteří nás dovedli až sem, a dychtivě očekávám, až budou ty zatracené multilineární mapy připraveny, abych mohl postavit své SMURF: 😆

Ale počkat, zmeškal jsem přednášku Victora Millera! 😭 Uvidíme, jestli odtamtud dokážu shrnout nějaké skvosty...

Victor Miller začíná pěkným citátem: "Štěstí přeje připraveným myslem!" 👌👌 Moje interpretace: Takže, přečtěte si co nejvíce kryptopapírů a učebnic matematiky?

"Zajímavé je, že když jsem se dostal na Harvard, byl jsem tam v té době jediným postgraduálním studentem [...] kteří skutečně měli nějaké možnosti s výpočty." Neciťte se sami.

Tolik matematiků. Nikdy jsem nechápal tu posedlost vyhýbat se smrti, ale pokud k tomu někdy existoval důvod... jde o to, abyste neztratili pokrok v matematice! (Co kdyby existoval jednodušší důkaz Fermatovy poslední věty?)

Victor zmínil Coppersmithův DL algoritmus pro GF(2^n) a jak začal přemýšlet o řešeních...

Proč v dnešní době 👇 všichni ověřujeme zkSNARKs za 1 milisekundu

V roce 2000 si někteří lidé zřejmě mysleli, že kryptografie eliptických křivek je mem. Povzbudivé pro blockchainy, říkám!

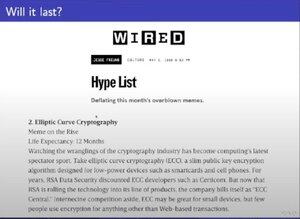
Victor dochází k závěru, že je vždy dobré studovat tajemné věci, jako jsou eliptické křivky nebo teorie čísel Nikdy nevíte, co bude skutečně praktické nebo užitečné o deset let později.

Zpět k přednášce Neala Koblitze: poprvé se dostal ke kryptografii v roce 1979 kvůli zvědavosti ohledně RSA! Chtěl lépe motivovat svůj kurz teorie čísel pro své studenty a myslel si, že RSA je skvělý způsob, jak toho dosáhnout! 💕

Později přišel Lenstrův algoritmus faktoringu eliptických křivek, který Koblitze 👇 opravdu uchvátil

Takže Koblitz začal přemýšlet: mohu použít tyto fantastické objekty algebraické geometrie ke "konstrukci" (spíše než k destrukci) kryptografie?

Koblitz vzpomíná, že dělání kryptoměn v té době bylo jakýmsi rebelským aktem. A tato živost a svobodomyslnost ukazovala: např. "omezení" na CRYPTO rump session znamenalo, že jste mohli na reproduktory 😂😂 házet pouze *prázdné* plechovky od piva

To se samozřejmě změnilo. Ale jak již dříve uvedl Dan Boneh, mělo by to být považováno za úspěch, který svědčí o tom, že se náš obor rozjel!

Dobře, dobře, tohle je opravdu konec! 🫡 Podívejte se na dvě nahrávky zde: A celý program zde: