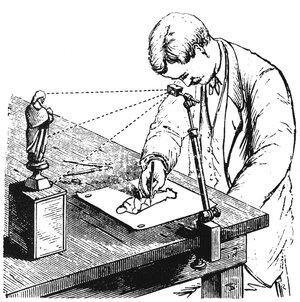
En "camera lucida" är en enhet som använder ett prisma som hålls av en metallarmatur för att projicera en bild av scenen framför den på ett papper under den, ungefär som en modern projektor ansluten till en live kameraström. Dessa uppfanns troligen i början av 1400-talet, även om publicerade uppgifter om dem inte dyker upp förrän i slutet av 1500-talet. En del av anledningen till detta är sannolikt att de var väl bevarade affärshemligheter för konstnärer som använde dem för att uppnå en grad av noggrannhet som tidigare var omöjlig eller åtminstone extremt svår att göra på en "frihand" utan hjälp. Konstnären David Hockney blev mycket intresserad av detta ämne för flera år sedan och skrev en bok om det 2001. Hans grundläggande teori var att den anmärkningsvärda förbättringen i noggrannhet och realism var direkt hänförlig till hemlig användning av camera lucida (och även en tidigare anordning som kallades camera obscura). Som han påpekade, före den perioden skulle du aldrig se en målning av en luta i perspektiv som inte såg förvrängd och fel ut. Även om man kunde använda "perspektivets regler" för att rita enkla rätlinjiga former realistiskt, var den mer komplexa geometrin hos en luta bortom normal mänsklig förmåga att avbilda realistiskt i rymden. Denna teori är känd som Hockney-Falco-tesen. Ända sedan jag lärde mig om detta på college i början av 2000-talet har jag på sätt och vis mentalt applicerat en asterisk på vissa målares verk. Till exempel, hur mycket jag än respekterar och beundrar Ingres och Caravaggio, dämpades min vördnad för deras färdigheter av insikten att de troligen använde sig av den här typen av mekanisk hjälp. Och visst, mycket av konstnärskapet ligger i konceptet, kompositionen och inramningen, färgerna, penseldragen etc. Men det var den hisnande verklighetstrogna realismen som imponerade mest på mig, och den delen av den krossades åtminstone delvis av denna uppenbarelse. Det fick mig också att respektera Michelangelos skulpturala realism ännu mer (och även hans studier som tydligt är skisser gjorda av livet). Anledningen till att jag tar upp detta är i alla fall att jag tror att vi är på väg att samma typ av saker ska hända inom matematiska forskningsområden i och med tillkomsten av modeller som GPT-5 Pro. Jag har redan använt den för att göra vad jag misstänker är genuint ny och intressant forskning (som jag har beskrivit i de senaste trådarna), och vi fick just idag en uppdatering från Sebastien Bubeck på OpenAI som visar att modellen kunde bevisa ett intressant resultat i samtida matematik med hjälp av ett nytt bevis, i ett enda skott inte mindre. Så är denna nya tidsålder plötsligt över oss. Vi har precis sett ett resultat från kinesiska datavetare som förra veckan slog ett rekord för optimal sortering som stod sig i 45 år. Jag funderade då på hur jag undrade om AI användes på något sätt för att generera det resultatet. Se också den senaste artikeln i den citerade tweeten, som har en liknande karaktär i det att den är både överraskande och samtidigt elementär. Dessa verkar för mig vara kännetecken för resultat som kan ha gynnats av AI på något sätt. Nu vill jag inte anklaga dessa författare för någonting. Så vitt jag vet gjorde de allt manuellt, precis som målarna på 1300-talet gjorde. Och även om de använde AI för att hjälpa dem, har vi ännu inte accepterat sedvänjor om hur vi ska hantera det: vilka avslöjanden som är berättigade och hur krediter ska fördelas och övervägas. Hela begreppet upphovsmannaskap måste omprövas i dag. I min senaste tråd där jag undersökte tillsammans med GPT-5 Pro om användningen av Lie-teori i djupinlärning, utformade jag uppmaningarna själv, även om jag aldrig på en miljon år skulle kunna generera den teori och kod som modellen utvecklade som ett resultat av dessa uppmaningar. Får jag äran för resultatet om det visar sig revolutionera fältet? Vad sägs om mitt efterföljande experiment, där jag använde mina ursprungliga uppmaningar som jag skrev själv tillsammans med en "metaprompt" för att få GPT-5 Pro att komma med ytterligare 10 par uppmaningar som var löst modellerade efter mina egna, men som involverade helt andra grenar av matematiken som utvecklades i helt olika riktningar. Får jag beröm för de teorierna om de visar sig vara viktiga? Jag hoppas verkligen det, eftersom jag redan har publicerat idéerna och koden på GitHub och publicerat dem brett, så om någon följer upp dessa frågeställningar skulle akademisk etik kräva att de citerar mig. Men även om du tycker att jag förtjänar beröm för att jag styr AI:n med min egen uppmaning, så är säkert mina anspråk på prioritet något försvagade för de 10 andra teorierna som är resultatet av att använda min uppmaning som en modell för metaprompting, eller hur? Jag visste trots allt inte ens att "Tropical Geometry" var en grej för ett par dagar sedan, men nu har jag en teori och kod som applicerar det på AI-forskning. Jag skulle vilja påstå att precis som jag mentalt började applicera en asterisk på vissa konstverk och konstnärer som liknar asterisken bredvid Barry Bonds namn i Hall of Fame, misstänker jag att de flesta forskare kommer att börja göra samma sak för alla nya matematiska teoribaserade artiklar under det kommande året eller så. Jag misstänker att folk snart nog kommer att säga saker som "den här killen är den äkta varan; han skrev sina bästa uppsatser före 2025!" för att skilja mellan de som gjorde allt sitt arbete manuellt med hjälp av sina egna hjärnor och de som använde AI-hjälp. Och det är absolut ett giltigt sätt att tänka på saker och ting om AI inte bara kan svara på svåra teoretiska problem utan till och med ställa de intressanta frågorna på egen hand. Om jag har rätt bör vi förbereda oss för en kommande tsunami av chockerande forskningsrapporter som slår gamla rekord och gränser, och som krossar murar som länge antogs vara relativt ogenomträngliga i brist på någon genombrottsteori. Och jag tror att många av dessa resultat kommer att ha något gemensamt: att de alltid fanns där framför oss, men att de krävde att man kombinerade teori från olika områden av matematik och tillämpade ämnen på nya sätt som inte hade tillämpats tidigare på grund av mänskliga, sociologiska skäl: olika fält som delades upp över linjer, med olika terminologi, tidskrifter, praktiker, avdelningar, konferenser, sociala nätverk etc. Den andra formen som jag misstänker att dessa resultat kommer att ta är att utnyttja elementära resultat på bisarra sätt som, av någon anledning, inte kommer naturligt för mänskliga hjärnor, men som vi kan förstå när de väl är tydligt förklarade för oss. En annan form de kan ta är resultat som utnyttjar sedan länge bortglömda esoterica från det sena 1800-talets analys. Den sortens knep som gjorde det möjligt för Feynman att lösa integraler som ingen annan kunde lösa. Dessa resultat är kända och finns i böcker, men ingen läser dessa böcker längre, och de ursprungliga teorierna som de utvecklades för har till stor del ersatts av vårt moderna maskineri som arbetar på många nivåer av ökad abstraktion och allmängiltighet. En annan form de kan ta är att helt enkelt tillämpa känd matematik som förstås av bara några hundra specialiserade genier i världen som bara fokuserar på teori och inte alls på tillämpningar. Denna matematik kan bara ha "legat och vänt" sedan 1950- eller 1970-talet och väntat på att någon ska tillämpa den på ett praktiskt problem som de inom AI-forskning. Många av de idéer som jag undersökte med GPT-5 verkar falla inom denna kategori.